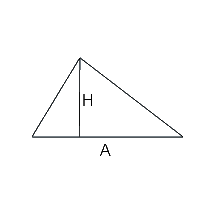Calculer l'aire d'un triangle rectangle
Calculer l’aire d’un triangle est un exercice classique de géométrie. Le principe est simple, il faut considérer le triangle comme la moitié d’une figure géométrique. Afin de développer précisément tous les cas, nous allons aborder le calcul de l’aire d’un triangle rectangle, le calcul de l’aire d’un triangle isocèle puis celle d’un triangle quelconque.
Cas d’un triangle rectangle
Le triangle rectangle est caractérisé par un angle droit (90 degrés). Ce triangle représente la moitié d’un rectangle. Pour calculer son aire, il suffit de calculer l’aire du rectangle et de le diviser par deux.
Explications en image :
Pour calculer l’aire du triangle rectangle (en bleu), il faut donc effectuer l’opération suivante (Côté A) x (Côté B) / 2.
Cas d’un triangle isocèle
Un triangle isocèle est un triangle qui a la particularité d’avoir 2 côtés de même longueur. L’aire d’un triangle isocèle se calcule en prenant la base du rectangle que l’on multiplie par la moitié de la hauteur. Il est important de préciser ce qu’est la base et la hauteur d’un triangle.
La base d’un triangle isocèle est le côté du triangle dont la longueur est différente de celle des deux autres. La hauteur d’un triangle isocèle est définie comme étant une droite qui coupe la base à angle droit et qui passe par le sommet des deux côtés de même longueur.
On peut donc conclure en disant qu’un triangle isocèle est composé de deux triangles rectangles.
L’aire du triangle est égale à deux l’aire d’un des triangles rectangles soit :
AIRE = 2 x [(Base / 2) x Hauteur /2] = (Base / 2) x Hauteur
Cas d’un triangle équilatéral
Un triangle équilatéral est un triangle qui a trois côtés égaux. Le calcul de l’aire d’un tel triangle est identique à celui du calcul d’un triangle isocèle.
Le principe est toujours le même, il faut tracer la hauteur du triangle afin de définir deux triangles rectangles. L’aire totale étant la somme des deux aires des triangles rectangles.
Comment calculer la hauteur d’un triangle ?
Un certain Monsieur Pythagore s’est penché sur cette question il y a très longtemps. Il créa un théorème à qui il donna son nom : le théorème de Pythagore. Cette formule est très connue des lycéens, elle indique que dans un triangle rectangle le carré de l’hypoténuse (le côté le plus long du triangle) est égal à la somme des carrés des deux autres côtés.
Les explications en image :
Le théorème énonce : C2 = A2 + B2
Dans un triangle quelconque A est la hauteur, il suffit d’extraire A de la formule :
A = racine carrée de (C2 - B2)
Nous vous proposons sur notre site un ensemble d'simulateurs dédiés à la géométrie, aux calculs d'aire, de surface, de volume, dont voici quelques exemples :
En complément de lecture sur le calcul de l'aire d'un triangle rectangle nous vous proposont les articles suivant: